Search

Software Engineer's Notes

Open Search
Category

Genel

Understanding Lookup Tables in Computer Science

When working with algorithms and data structures, efficiency often comes down to how quickly you can retrieve the information you need. One of the most powerful tools to achieve this is the Lookup Table. Let’s break down what it is, why we need it, when to use it, and the performance considerations behind it.

What is a Lookup Table?

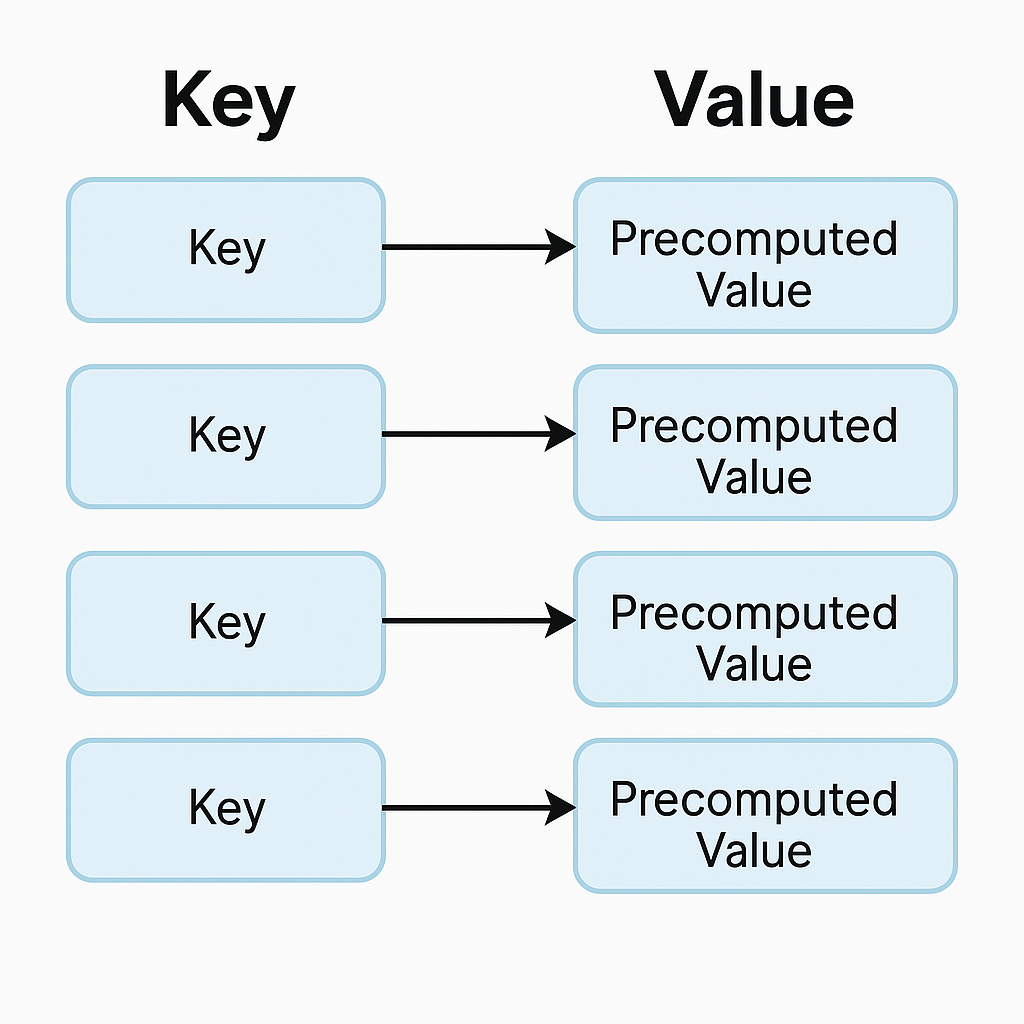
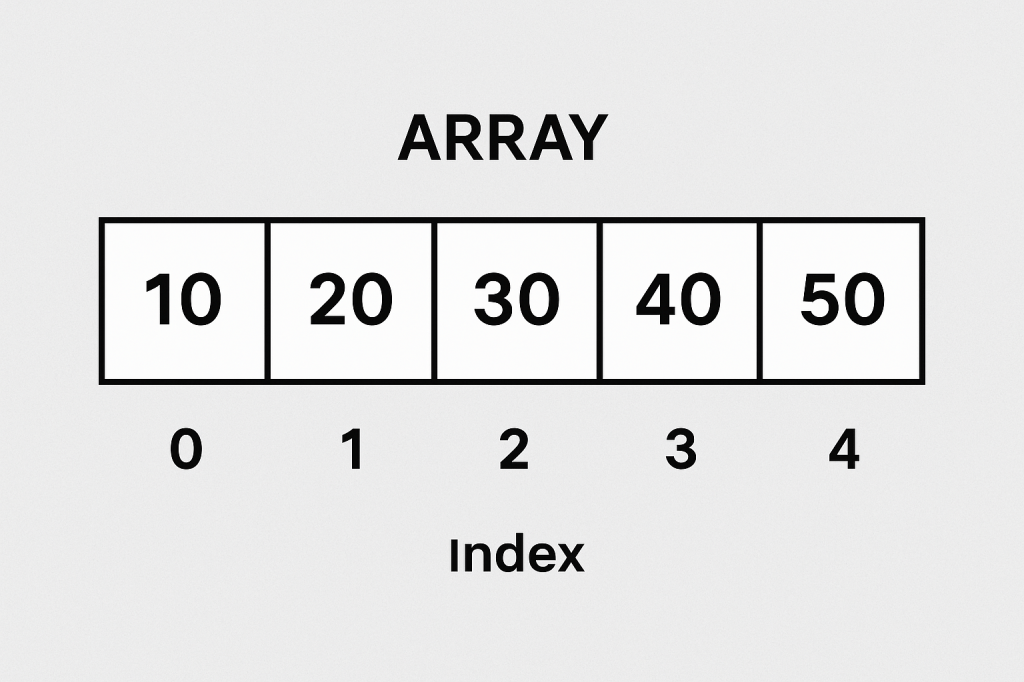
A lookup table (LUT) is a data structure, usually implemented as an array, hash map, or dictionary, that allows you to retrieve precomputed values based on an input key. Instead of recalculating a result every time it’s needed, the result is stored in advance and can be fetched in constant time.

Think of it as a cheat sheet for your program — instead of solving a problem from scratch, you look up the answer directly.

Why Do We Need Lookup Tables?

The main reason is performance optimization.
Some operations are expensive to compute repeatedly (e.g., mathematical calculations, data transformations, or lookups across large datasets). By precomputing the results and storing them in a lookup table, you trade memory for speed.

This is especially useful in systems where:

  • The same operations occur frequently.
  • Fast response time is critical.
  • Memory is relatively cheaper compared to CPU cycles.

When Should We Use a Lookup Table?

You should consider using a lookup table when:

  1. Repetitive Computations: If the same calculation is performed multiple times.
  2. Finite Input Space: When the possible inputs are limited and known beforehand.
  3. Performance Bottlenecks: If profiling your code shows that repeated computation is slowing things down.
  4. Real-Time Systems: Games, embedded systems, and graphics rendering often rely heavily on lookup tables to meet strict performance requirements.

Real World Example

Imagine you are working with an image-processing program that frequently needs the sine of different angles. Computing sine using the Math.sin() function can be expensive if done millions of times per second.

Instead, you can precompute sine values for angles (say, every degree from 0° to 359°) and store them in a lookup table:

double[] sineTable = new double[360];
for (int i = 0; i < 360; i++) {
    sineTable[i] = Math.sin(Math.toRadians(i));
}

// Later usage
double value = sineTable[45]; // instantly gets sine(45°)

This way, you retrieve results instantly without recalculating.

Time and Memory Complexities

Let’s analyze the common operations in a lookup table:

  • Populating a Lookup Table:
    • Time Complexity: O(n), where n is the number of entries you precompute.
    • Memory Complexity: O(n), since you must store all values.
  • Inserting an Element:
    • Time Complexity: O(1) on average (e.g., in a hash map).
    • Memory Complexity: O(1) additional space.
  • Deleting an Element:
    • Time Complexity: O(1) on average (e.g., marking or removing from hash table/array).
    • Memory Complexity: O(1) freed space.
  • Retrieving an Element (Lookup):
    • Time Complexity: O(1) in most implementations (arrays, hash maps).
    • This is the primary advantage of lookup tables.

Conclusion

A lookup table is a powerful optimization technique that replaces repetitive computation with direct retrieval. It shines when input values are limited and predictable, and when performance is critical. While it requires additional memory, the trade-off is often worth it for faster execution.

By understanding when and how to use lookup tables, you can significantly improve the performance of your applications.

Understanding Stacks in Data Structures

When learning about data structures, one of the simplest yet most powerful concepts is the stack. Just like its real-world counterpart—a stack of plates in your kitchen—this structure follows a very specific order for adding and removing items. Let’s dive deeper into what stacks are, why we need them, and where they shine in real-world applications.

What is a Stack?

A stack is a linear data structure that follows the LIFO (Last In, First Out) principle.

  • Last In → The last element added to the stack will be the first one removed.
  • First Out → The element added earliest will only be removed once everything added after it is removed.

Think of it as a pile of books—if you put a book on top, it’s the first one you’ll remove.

Stacks typically support two main operations:

  • Push → Add an element to the top.
  • Pop → Remove the element from the top.

Why Do We Need Stacks?

Stacks are crucial because they help us manage data in an order-dependent way. Their restricted operations make them predictable and efficient for solving problems where order of processing matters. Some common reasons we need stacks:

  • Managing function calls in programming (call stack).
  • Undo/redo functionality in applications.
  • Parsing expressions and checking balanced parentheses.
  • Backtracking algorithms (mazes, puzzles, etc.).

When Should We Use a Stack?

You should use a stack when:

  • You need to process elements in reverse order of their arrival.
  • You want a controlled way to temporarily store items.
  • You need fast insertion and removal at one end only.

If your use case involves removing items in the same order they were added, a queue (FIFO) might be more suitable.

A Real-World Example

Consider the browser back button.

  • Each time you visit a new page, the URL is pushed onto a stack.
  • When you press the back button, the last visited page is popped off, and the browser takes you to the previous one.

This is a perfect example of LIFO behavior in everyday life.

Time and Memory Complexities

Stacks are highly efficient since most operations occur at the top of the structure:

  • Pushing (insertion): O(1) – constant time.
  • Popping (deletion): O(1) – constant time.
  • Peeking (viewing top element): O(1) – constant time.
  • Memory complexity: O(n) – proportional to the number of elements stored.

This makes stacks a great fit when you need quick and predictable operations.

Final Thoughts

Stacks may sound simple, but they form the foundation of many critical systems in computer science. From managing program execution to enabling undo features in your favorite text editor, stacks are everywhere. Mastering them is a big step in becoming a stronger programmer.

Understanding ArrayLists in Programming

When working with data in programming, choosing the right data structure is critical. One of the most flexible and widely used data structures is the ArrayList. In this post, we’ll explore what ArrayLists are, why we need them, when to use them, and their time and memory complexities—with a real-world example to tie it all together.

What is an ArrayList?

An ArrayList is a resizable array implementation provided in many programming languages (for example, java.util.ArrayList in Java or List<T> in C#). Unlike regular arrays that have a fixed size, ArrayLists can grow and shrink dynamically as elements are added or removed.

Think of an ArrayList as a dynamic array that provides built-in methods for managing data efficiently.

Why Do We Need an ArrayList?

Arrays are powerful, but they come with limitations:

  • Fixed size: once created, their size cannot change.
  • Manual resizing: you need to manage memory and copy elements if more space is needed.

ArrayLists solve these problems by:

  • Automatically resizing when more elements are added.
  • Providing handy methods like add(), remove(), contains(), and get() for easier management.
  • Allowing both random access (like arrays) and dynamic growth.

When Should We Use ArrayLists?

You should use an ArrayList when:

  • The number of elements in your collection is not known in advance.
  • You frequently need to add, remove, or search for elements.
  • You want random access to elements by index.
  • Performance is important, but you can tolerate occasional resizing overhead.

If you know the size in advance and memory efficiency is critical, a simple array might be better. But if flexibility matters, ArrayLists are the way to go.

Real-World Example of an ArrayList

Imagine you’re building a shopping cart in an e-commerce application.

  • Users can add items (products).
  • They can remove items at any time.
  • The cart needs to expand dynamically as users shop.

Here’s a Java snippet:

import java.util.ArrayList;

public class ShoppingCart {
    public static void main(String[] args) {
        ArrayList<String> cart = new ArrayList<>();

        // Adding items
        cart.add("Laptop");
        cart.add("Smartphone");
        cart.add("Headphones");

        System.out.println("Cart: " + cart);

        // Removing an item
        cart.remove("Smartphone");
        System.out.println("Cart after removal: " + cart);

        // Accessing an item
        System.out.println("First item: " + cart.get(0));
    }
}

Output:

Cart: [Laptop, Smartphone, Headphones]
Cart after removal: [Laptop, Headphones]
First item: Laptop

This example shows how ArrayLists let us manage collections dynamically without worrying about resizing manually.

Time and Memory Complexities

Understanding performance helps you make better design decisions. Here are the typical complexities for ArrayLists:

  • Populating (adding at the end):
    • Average case: O(1) (amortized constant time)
    • Worst case (when resizing happens): O(n)
  • Inserting an element at a specific index:
    • O(n) (because elements may need to shift)
  • Deleting an element:
    • O(n) (elements after the removed one shift left)
  • Accessing an element by index:
    • O(1) (direct access like an array)
  • Memory usage:
    • Slightly higher than arrays due to dynamic resizing overhead (extra space allocated to reduce frequent copying).

Conclusion

ArrayLists are one of the most useful data structures for everyday programming. They combine the fast access of arrays with the flexibility of dynamic collections. Whether you’re building a shopping cart, managing user sessions, or keeping track of tasks, ArrayLists provide a balance of performance and convenience.

Next time you’re faced with a growing list of elements, consider reaching for an ArrayList—it just might be the perfect fit.

Understanding Linked Lists: A Beginner’s Guide

When learning data structures, arrays are usually the first stop. But once you’ve mastered them, you’ll quickly discover a new structure that solves many of their limitations: the linked list.

In this blog, we’ll explore what a linked list is, why we need it, when to use it, provide a real-world example, and analyze the time and memory complexities of linked lists.

What is a Linked List?

A linked list is a linear data structure where elements (called nodes) are stored in separate memory locations and connected using pointers (links).

Each node typically contains:

  • Data – the value you want to store
  • Pointer/Reference – an address pointing to the next node in the list

Unlike arrays, linked lists do not store elements in contiguous memory blocks.

Why Do We Need Linked Lists?

Arrays are simple and efficient for random access, but they come with drawbacks:

  • Fixed size (in most programming languages, arrays cannot grow dynamically without creating a new one)
  • Costly insertions and deletions (shifting elements takes time)

Linked lists solve these issues by:

  • Allowing dynamic memory allocation (they grow and shrink as needed)
  • Enabling fast insertions and deletions without shifting entire elements

When Should We Use Linked Lists?

You should consider linked lists when:

  • Memory is fragmented, and you can’t allocate a large contiguous block (required for arrays).
  • You expect frequent insertions and deletions, especially in the middle of the collection.
  • Random access is not a priority (linked lists are slower at accessing an element by index).

Real-World Example

Imagine a music playlist app.

  • Songs can be dynamically added or removed from the playlist.
  • You don’t know the total number of songs in advance.
  • You often skip to the next song (which is just following the pointer to the next node).

Here, a linked list structure is perfect because it supports efficient insertions, deletions, and sequential traversal.

Time & Memory Complexities

Here’s a quick overview of linked list operations:

OperationTime ComplexityExplanation
Populate (building a linked list of n elements)O(n)Each element needs to be inserted one by one
Insertion at headO(1)Just update the head pointer
Insertion at tailO(1) (if tail pointer is maintained) / O(n) (if not)Depends on whether you track the tail
Insertion in middleO(n)Need to traverse to the correct position
Deletion at headO(1)Update head pointer
Deletion at tailO(n)Need to traverse to the last element
Deletion in middleO(n)Traverse to find node, then remove
Access by indexO(n)Must traverse sequentially
Memory usageHigher than arraysEach node requires extra space for a pointer

Conclusion

Linked lists are powerful when dealing with dynamic data where frequent insertions and deletions occur. However, they trade off speed for random access and consume more memory due to pointers.

Understanding when to use arrays and when to use linked lists is a core skill every software engineer should master.

Understanding Arrays: A Complete Beginner’s Guide

Arrays are one of the most fundamental concepts in computer science and programming. Whether you are working with Java, Python, JavaScript, or PHP, arrays play a critical role in how data is stored and accessed. In this post, we’ll break down what arrays are, why they’re important, when to use them, and even analyze their performance.

What is an Array?

An array is a data structure that stores multiple values of the same type in a single variable. Instead of declaring multiple variables to hold related data, we can store them in an array and access them by their index (position).

Example in Java:

int numbers[] = {10, 20, 30, 40, 50};
System.out.println(numbers[2]); // prints 30

Here, numbers[2] refers to the third element in the array (since arrays are zero-indexed).

Why Do We Need Arrays?

Arrays solve the problem of managing large amounts of data efficiently. Without arrays, we would need to create separate variables for each value, which becomes unmanageable.

  • Organized data storage – Store related items together.
  • Fast access – Retrieve elements in constant time using an index.
  • Efficient looping – Easily iterate over items with for or while loops.

When Should We Use Arrays?

Use arrays when:

  • You know the fixed size of data in advance.
  • You want fast, random access to elements by index.
  • You want to perform repetitive operations on similar data types.

However, if the dataset size changes frequently (lots of insertions/deletions), arrays may not be the best choice. In such cases, dynamic structures like ArrayList in Java or List in Python are preferred.

Real-World Example of Arrays

Imagine a system that stores the grades of students in a class:

grades = [85, 90, 78, 92, 88]

# Find average grade
average = sum(grades) / len(grades)
print("Class Average:", average)

Instead of creating five different variables (grade1, grade2, grade3...), an array helps us store all grades in a single variable and compute results easily.

Time and Memory Complexity

Arrays are efficient but come with tradeoffs. Let’s look at their common operations:

OperationTime ComplexityMemory Impact
Access (arr[i])O(1)No extra memory
Update (arr[i] = x)O(1)No extra memory
Populate (initial fill)O(n)O(n) space
Insert (middle)O(n)May shift elements
Insert (end)O(1) (if space) / O(n) (resize)Extra memory if resized
Delete (middle)O(n)Shift elements left
Delete (end)O(1)No shift

Key takeaway: Arrays are excellent for fast access but not ideal for frequent insertions or deletions in the middle.

Conclusion

Arrays are the backbone of many algorithms and data structures. They provide an easy way to store, organize, and access data efficiently. While they shine in random access speed, they are less suitable when frequent modifications are needed. Understanding arrays is the first step toward mastering more advanced structures like linked lists, stacks, and queues.

Understanding Theta (Θ) Notation in Algorithms

Understanding Theta (Θ) Notation in Algorithms

When we study algorithms, we often come across notations like Big O, Omega, and Theta. Among these, Theta (Θ) plays a special role because it gives us a tight bound on the performance of an algorithm. Let’s explore what it means, why it matters, and how you can use it in practice.

What is Theta (Θ) Notation?

Theta notation (Θ) describes the asymptotically tight bound of an algorithm.
In simple words, it tells us both:

  • The upper bound (how slow it can get in the worst case), and
  • The lower bound (how fast it can get in the best case).

When we say f(n) ∈ Θ(g(n)), it means that f(n) grows at the same rate as g(n) for large input sizes.

Why is Theta Notation Important?

  1. Precise analysis – Unlike Big O (which only shows the worst-case growth), Theta captures the exact growth rate.
  2. Realistic performance – It helps us understand how an algorithm will perform on average and in practice.
  3. Comparison – It gives a fair way to compare algorithms beyond just the worst case.

For example, if an algorithm runs in Θ(n log n) time, it means no matter what, the runtime will grow proportionally to n log n.

How Can I Use Theta Notation?

  • Algorithm design: When choosing between two approaches, knowing their Θ complexity helps make the best decision.
  • Performance prediction: You can predict how your code will scale with larger inputs.
  • Interview preparation: Many technical interviews expect you to provide Θ complexity for your solutions.

How Do I Calculate Θ?

To calculate Θ:

  1. Identify the basic operations of your algorithm (comparisons, additions, recursive calls, etc.).
  2. Count how many times those operations run with input size n.
  3. Express the count as a mathematical function f(n).
  4. Simplify the function and compare it to a common class (e.g., n, n log n, n²).

Real-World Example of Θ Calculation

Let’s take the task of checking if a number exists in a phone contact list:

  • Suppose the contact list is stored as a sorted array of names.
  • If you use binary search, at each step you cut the search space in half.
  • For n contacts, the number of steps is about log n.
  • Therefore, the runtime is Θ(log n).

No matter how the data looks, you will always need about log n steps. That’s why binary search is tightly bound by Θ(log n).

Θ vs Big O: What’s the Difference?

  • Big O (O): Gives an upper bound (how bad it can get).
  • Big Omega (Ω): Gives a lower bound (the best it can do).
  • Theta (Θ): Captures both bounds → it’s the tight bound.

So, if an algorithm is O(n²) and also Ω(n²), then it is Θ(n²).

Conclusion

Theta notation is the most precise way to describe algorithm efficiency.
It gives you a complete picture of how your program scales. Whether you are learning computer science fundamentals or preparing for coding interviews, mastering Θ notation will make your understanding of algorithms stronger.

Diagram: Contrasting O, Ω, Θ

0

Ω (Omega) Notation — The Asymptotic Lower Bound

What is Ω-notation?

Ω (Omega) provides a lower bound on algorithm complexity. It tells us the minimum resources (time, comparisons, operations) an algorithm will always need as the input grows.

f(n) ∈ Ω(g(n)) ⇔ ∃ c greater than 0, n₀ ≥ 0 : f(n) ≥ c · g(n), ∀ n ≥ n₀

Why is it important?

  • Guarantees performance: tells us the least amount of work required.
  • Proves impossibility: For many problems, no algorithm can beat a known lower bound (e.g., comparison sorting is Ω(n log n) → no algorithm can beat it.)
  • Supports tight bounds: combine with Big-O to get Θ (tight asymptotics).

How do we use it?

  • To prove a minimum baseline cost (e.g., reading input is Ω(n)).
  • To establish theoretical limits for problem classes.
  • To compare efficiency: if your algorithm is O(n log n) and the problem is Ω(n log n), then your algorithm is optimal.

How do we calculate Ω?

1. Dominant-term method

Keep the leading term of a polynomial.
Example:

4n^3 + 2n^2 + 5 ∈ Ω(n^3)

2. Inequality bounding

Show f(n) ≥ c · g(n) beyond some n₀.

3. Limits

If

then f ∈ Ω(g).

Step-by-step examples

Example 1: Polynomial

f(n) = 3n^2 + 10n + 5
  1. For n ≥ 1, 10n + 5 ≥ 0.
  2. So f(n) ≥ 3n².
  3. Pick c = 3, n₀ = 1.

Conclusion:

f(n) ∈ Ω(n^2)

Example 2: Code Snippet (Java)

int count = 0;
for (int i = 1; i <= n; i++) {
    for (int j = i; j <= n; j++) {
        count++;
    }
}
  • Inner loop runs (n - i + 1) times.
  • Total = n(n+1)/2.
  • ≥ n²/2 ⇒ Ω(n²).

Relationship with Big-O and Θ

  • O(g): upper bound (at most).
  • Ω(g): lower bound (at least).
  • Θ(g): tight bound (both O and Ω).

Diagram: Contrasting O, Ω, Θ

0

Big-O Notation: A Friendly, Practical Guide

What is Big-O notation?

Big-O notation describes how an algorithm’s running time or memory grows as the input size n gets large.
It gives an upper bound on growth—e.g., “this algorithm runs in O(n log n) time,” meaning its time won’t grow faster than some constant × n log n for large n. Big-O ignores machine details and constants so we can compare algorithms by their shape of growth, not their exact milliseconds on one computer.

Why Big-O matters

  • Scalability: Today’s data set fits in RAM; tomorrow’s is 100× bigger. Big-O tells you who survives that jump.
  • Design choices: Helps choose the right data structures/approaches (hash table vs. tree, brute-force vs. divide-and-conquer).
  • Performance budgeting: If your endpoint must answer in 50 ms at 1M records, O(n²) is a red flag; O(log n) might be fine.
  • Interview lingua franca: It’s the common vocabulary for discussing efficiency in interviews.

How to calculate Big-O

  1. Define the input size n. (e.g., length of an array, number of nodes.)
  2. Count dominant operations as a function of n (comparisons, swaps, hash lookups, etc.).
  3. Focus on worst-case unless stated otherwise (best/average can be different).
  4. Drop constants and lower-order terms. 3n² + 2n + 7 → O(n²).
  5. Use composition rules:
    • Sequential steps add: O(f(n)) + O(g(n)) → O(f(n) + g(n)), usually dominated by the larger term.
    • Loops multiply: a loop of n iterations doing O(g(n)) work → O(n · g(n)).
    • Nested loops multiply their ranges: outer n, inner n → O(n²).
    • Divide-and-conquer often yields recurrences (e.g., T(n)=a·T(n/b)+O(n)) solved via the Master Theorem (e.g., mergesort → O(n log n)).

Step-by-step example: from counts to O(n²)

Goal: Compute the Big-O of this function.

def count_pairs(a):        # a has length n
    total = 0              # 1
    for i in range(len(a)):           # runs n times
        for j in range(i, len(a)):    # runs n - i times
            total += 1                 # 1 per inner iteration
    return total           # 1

Operation counts

  • The inner statement total += 1 executes for each pair (i, j) with 0 ≤ i ≤ j < n.
    Total executions = n + (n-1) + (n-2) + … + 1 = n(n+1)/2.
  • Add a few constant-time lines (initialization/return). They don’t change the growth class.

Total time T(n) is proportional to n(n+1)/2.
Expand: T(n) = (n² + n)/2 = (1/2)n² + (1/2)n.
Drop constants and lower-order terms → O(n²).

Takeaway: Triangular-number style nested loops typically lead to O(n²).

(Bonus sanity check: If we changed the inner loop to a fixed 10 iterations, we’d get n*10 → O(n).)

Quick Reference: Common Big-O Complexities

  • O(1) — constant time (hash lookup, array index)
  • O(log n) — binary search, balanced BST operations
  • O(n) — single pass, counting, hash-map inserts (amortized)
  • O(n log n) — efficient sorts (mergesort, heapsort), many divide-and-conquer routines
  • O(n²) — simple double loops (all pairs)
  • O(2ⁿ), O(n!) — exhaustive search on subsets/permutations

Big-O growth graph

The chart above compares how common Big-O functions grow as n increases. The y-axis is logarithmic so you can see everything on one plot; on a normal (linear) axis, the exponential curve would shoot off the page and hide the differences among the slower-growing functions.

  • Flat line (O(1)): work doesn’t change with input size.
  • Slow curve (O(log n)): halves the problem each step—scales very well.
  • Straight diagonal (O(n)): time grows linearly with input.
  • Slightly steeper (O(n log n)): common for optimal comparison sorts.
  • Parabola on linear axes (O(n²)): fine for small n, painful past a point.
  • Explosive (O(2ⁿ)): only viable for tiny inputs or with heavy pruning/heuristics.

0

MIRTH CONNECT – Parsing HL7

We can parse HL7 messages inside the transformer. We need to loop through the HL7 and check the Segment types. When we find the correct segment, we can read the data from the target element.

Continue reading “MIRTH CONNECT – Parsing HL7” →

0

Blog at WordPress.com.

Up ↑